The body movement function that uses musculature for deliberate and organized movement in space is called locomotion. The fundamental functional difference between the muscles involved in locomotion and the muscles responsible for the movement of the heart, face, sphincters, arteries etc., is the direct interface with the bones of the skeleton through the leverage mechanism.

The understanding of the leverage system is of paramount importance for strength and conditioning professionals. The basic definitions are as follows:

Lever – a rigid or semi-rigid beam (bone) resting on the pivot (joint) and applies force to the load at one end (heavy object) when pressure is applied to the other end (muscle action) through rotation around its fulcrum (load supporting joint), (Figure 1).

Figure 1: A lever transmitting point force through its length and tangential to the rotation arc (F_A – force applied; M_AF – moment arm of force applied; F_R – resistance force; M_R – the moment arm of the resistance force) [1].

Fulcrum – The point of pivot of the lever.

Muscle Force – Force produced by either a biochemical reaction or noncontractile tissue stretching, which results in the shortening of the muscle body, drawing opposite ends towards each other.

Resistance force – an external force acting on the body and opposing the muscle force (i.e., friction, inertia, gravity etc.)

Three types of levers

First-class lever – A condition when both resistive and the muscle forces are acting on the opposing sides of the fulcrum (Figure 2)

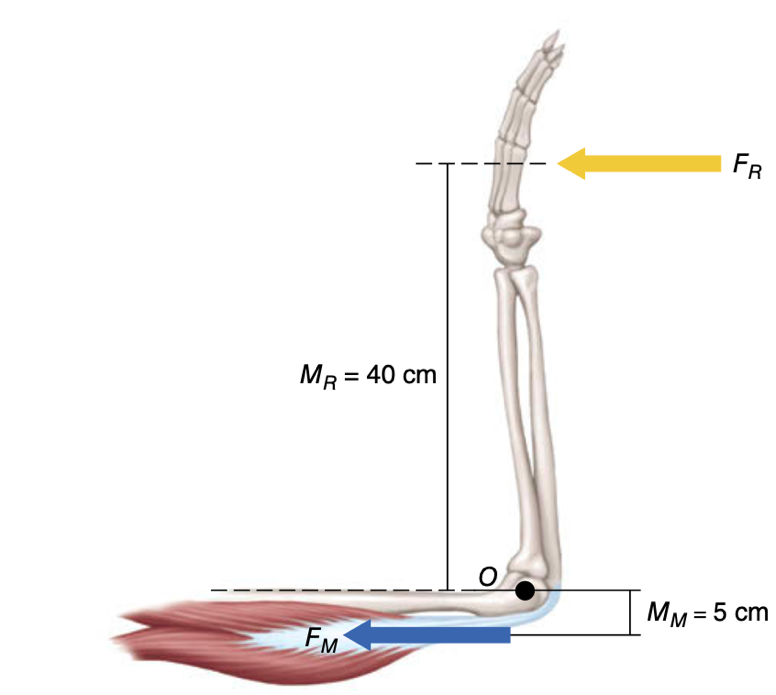
Figure 2: Forearm representing the 1st class lever (F_R – resistance force; MR – moment arm of resistive force; O – fulcrum; M_M – moment arm of muscle force) [1].

Second class lever – A lever that encounters both external load and muscle-exerted forces acting on the same side of the fulcrum, where the muscle moment arm is longer than its counterpart generated by external force and requires less force to counteract or overcome its resistive load (i.e., the action of calf muscles, due to its large moment arm have a great mechanical advantage when raising the body weight using a foot plantar-flexion mechanism).

Third-class lever – A lever where the muscle moment arm is shorter than the external load. This means that the second-class lever always has a mechanical advantage of < 1.0. This means that to equalise the two acting in opposite direction torque values, the muscle force must be greater than the resistance force (i.e., biceps require generating more significant force than its distal opponent (weight) when the demand is to produce forearm/elbow flexion torque while holding a heavy object).

Mechanical advantage 

The ratio between the moment arms of applied and resistive forces (M_AF / M_RF in Figure 1). Therefore, the equilibrium state is achieved when the products of forces and corresponding moment arms generated by resistive load and involved muscle(s) are equal. This can be represented as a ratio of 1.0 (for every 1 Newton of the resistance force, the muscle must generate 1 Newton of counteracting force, or greater, if required to move the object).

The ratio of moment arms > 1.0 indicates the presence of mechanical advantage, allowing for musculature (applied) force to be less than the resistive force for the same amount of torque (Torque = Force (Fm) x Moment Arm). When conversely, the mechanical advantage is < 1.0, the musculature must generate a greater amount of force than imposed by the resistive counterpart, therefore being in a state of disadvantage.

An excellent example of an equilibrium state would be a person holding a ball or a dumbbell in a partially flexed arm position. The reason for considering the partial flexion in this example is that during the full extension, the joint would usually be locked, resulting in the geometry-based mechanical advantage that will take the load off the musculature or distribute the load over the musculoskeletal structure, resulting in a complex combination of leverage. A typical example is when the front shoulder and upper trapezius muscles share the load during biceps curls. At the same time, the primary elbow flexors may come to complete rest during full extension of the joint.

Another excellent example of the geometric advantage is a classic leg press during which the quadriceps muscle group must work very hard to maintain a resistive force in equilibrium (holding the weight in knee and hip flexed position). However, the more significant the extension angle is applied, the shorter the moment arm of the resistive force.

Therefore, it becomes easier to hold the weight in equilibrium. Going further into full knee extension (when the angle between the femur and tibia is approximately 180 degrees (joint locked), the force is said to have zero moment arm and applied in an axial direction that is entirely supported by the skeleton structure and stabilising muscles around it (the act of balance). The primary movers are offloaded here, with the resistance force equally distributed through the rigid skeleton.

Understanding this kinematic relationship between interacting forces and geometry between muscle attachments and skeletal structures will help the S&C coach effectively design the programme and appropriate technique adjustments based on the athlete’s characteristics (body type, geometry etc.). It will also enable a coach to understand the sport’s specific demands and integrate these needs into strength training.

Moment arm 

A distance between the axis of the joint and perpendicularly applied vector force (also called lever arm). The larger lever arm generates greater torque in the joint, resulting in a greater mechanical advantage. Understanding this geometry plays a major role in coaches’ ability in exercise selection and modification, exposing athletes or patients to an appropriate type and quantity of load, and emphasising certain joints while offloading others.

A simple example would be finding the proper barbell position within the spectrum between the front and low-back squats (Figure 3). This adjustment of barbell position is often driven by several aspects, such as the individual morphology of an athlete (geometric proportions of bones), emphasis on targeted muscle groups and joints as weakness or injury-specific domain, or sport-specific demand.

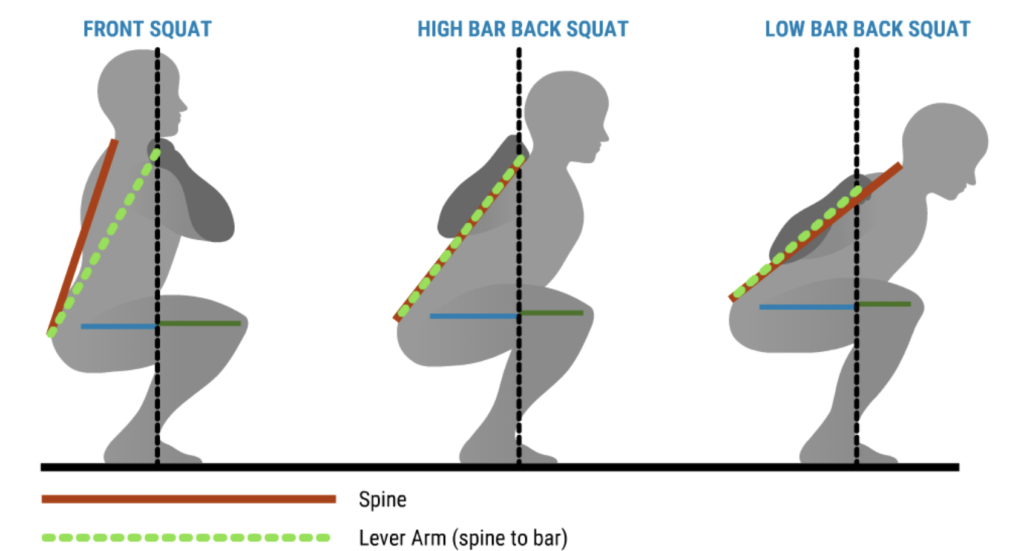
Figure 3: Spine-to-bar moment arm variations in a) front squat, b) high bar back squat, and c) low bar back squat [2].

Torque (also known as moment): 

The propensity of a force to cause an item to spin about a given fulcrum. It is quantified as the product of the force’s magnitude and the moment at arm’s length. 

Because muscle and resistance forces acting on the opposite side of the fulcrum, Figure 2 depicts a first-class lever, where: F_M x M_M = F_R x M_R occurs with isometric effort or constant-speed joint rotation.

Since M_M is significantly smaller than M_R, the F_M must be significantly larger than F_R, highlighting how unfavourable this arrangement is (i.e., a muscle must produce a comparatively large amount of force to anticipate a significantly smaller resistive force).

Most primary limb-moving muscles in the human body (acting on proximal joints) operate at a low mechanical advantage of < 1.0. Because of this, the output forces of these muscles are substantially higher than the forces imposed by the external object.

For instance, from figure 2, the muscle forces required to be greater than the resistive force by the factor of 8 since its moment arm is eight times smaller (shorter lever) than the resistive force applied to the hand.

The exceedingly high internal stresses that muscles and tendons endure during the fast and explosive activities of sports are often resulting consecutive damage to these tissues.

In real life, when the lever is in motion, its classification into 1^st, 2^nd or 3^rd types is a subjective and arbitrary choice, depending on where the fulcrum is located at any given moment since the actual force production mechanism can be a part of the complex kinetic chain and consist of a combination of livers that work altogether in a free-movement environment.

Since the musculoskeletal positioning/angles are constantly changing during the motion, the moment arm forces and their proportional interactions with the load will also change.

The following examples describe such dynamic interactions:

The location of the rotating axis fluctuates continuously through the range of joint motion for such movements as knee flexion and extension since the joint is not a true hinge. This course of motion influences the length of the moment arm through which the quadriceps and hamstrings function.

The patella (kneecap) prevents significant changes in the mechanical advantage of the quadriceps during the knee extension by preventing the quadriceps tendon from slipping too close to the axis of rotation. On the other hand, when considering elbow joint flexion and extension movement, the joint does not have a patella-like mechanism but rather has a tendon line of action that is relatively constant when disregarding the total limb movement, including the shoulder joint.

As already covered by the squat and leg extension mechanic’s earlier example, it can be appreciated that the moment arms of the load will constantly change throughout the movement following the alterations in joints angle. When utilising the free weights during resistance training, it should be considered that the weight mass is acting vertically down. However, its moment arms are equal to the horizontal distance between the centre of the object mass and the body joint around which rotation occurs. Thus, the resistive moment arm will vary with the joint angle throughout the movement (Figure 4).

Figure 4: Continuous change in moment arm through the arc of the lifting movement – the torque varies with the horizontal distance (moment arm) between elbow and weight [1].

Taking the matter one step further from the “schoolbook” case to the complex reality, we must consider other body soft tissues, such as fascia and aponeurosis, that form the series of biologically interacting pulleys and cables with fluid and dynamically adaptable properties.

Figure 5 demonstrates the more realistic force-vector distribution within the elbow joint compared to the simplified case in Figure 4. It shows the angular contribution of the bicipital aponeurosis to both the moment arm (due to contribution to bicipital distal tendon retraction [3] and overall load distribution during the elbow flexion/extension. One of the large practical implications of this knowledge may be more evident during injury management and treatment.

Figure 5: Bicipital aponeurosis contributing to change in moment arm and force distribution through the arc of the lifting movement – the torque varies with the horizontal distance (moment arm) between elbow and weight [3].

To summarise this discussion, it is essential to comprehend the mechanical advantage principle with all the participants, allowing the decomposition of biomechanical needs and projection into the corresponding strength training programme. Understanding movement kinematics explains why movement technique is subjective, where one size will not fit all.

Although learning basic principles of strength training techniques is fundamental, it may not necessarily guarantee success without specific adjustments based on individual and sport-specific requirements.

The Author: Ivan Usenko

Ivan Usenko is a sports performance scientist, mentor, and coach with diverse experience across disciplines and industries.

Ivan has over 20 years of experience in sports and fitness as an athlete, coach, and therapist for disciplines including track and field, tennis, rugby, martial arts, equestrian sports, and others. He is a member of the UK Southwest Athletics Coaching Network and UK Athletics (UKA).